We approach a problem of reconstruction of missing data in a time-frequency transform in the particular case where these are the phases of the coefficients of this transform. We assume that the locations of the coefficients for which they are missing phases are known. We call this problem: phase inpainting in the time-frequency plane . We formulate it mathematically, then we propose three algorithms to solve it. The proposed theoretical and algorithmic developments are described in references 1 and 2.
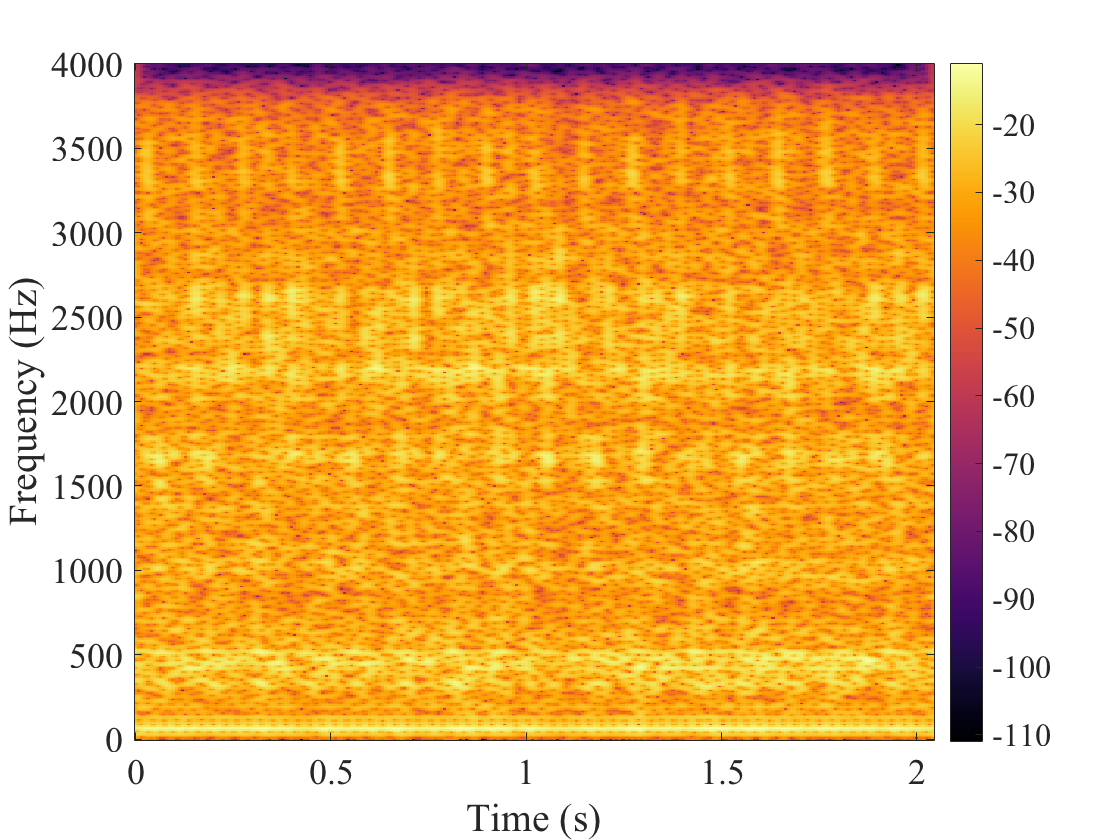
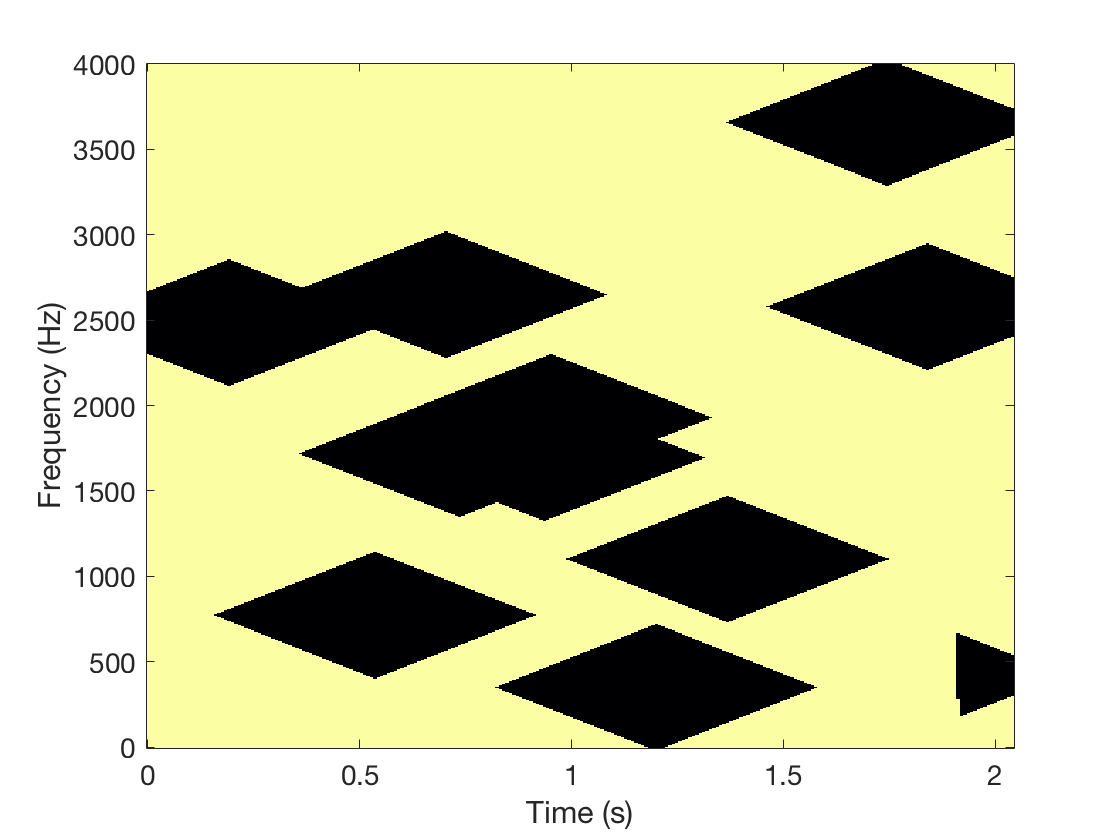
In this experiment, the mask that illustrates the masked region is generated by considering masked regions of width 15. By width, we mean the diameter of the masked regions in number of time-frequency coefficients. The locations of these regions are generated randomly according to a uniform distribution on the time-frequency lattice. We set the percentage of missing phases to 40% and conducted two experiments, one where the signal of interest is respectively the car engine sound and the bird song. We tested our GLI method (Griffin and Lim for phase Inpainting) on these data. As a comparison, we compute a reference solution named RPI (Random phase inapinting) which consists in replacing the missing phases by random phases and in reconstructing the signal. Theoretical results and comparisons of all our methods can be found in references 1 and 2. But here, we only compare GLI and RPI on real audio signals. The binary masks and the respective spectrograms are shown below.


| Original car sound | Sound with 40 % missing phases | RPI | GLI |
|---|---|---|---|
|
|
|
|
|
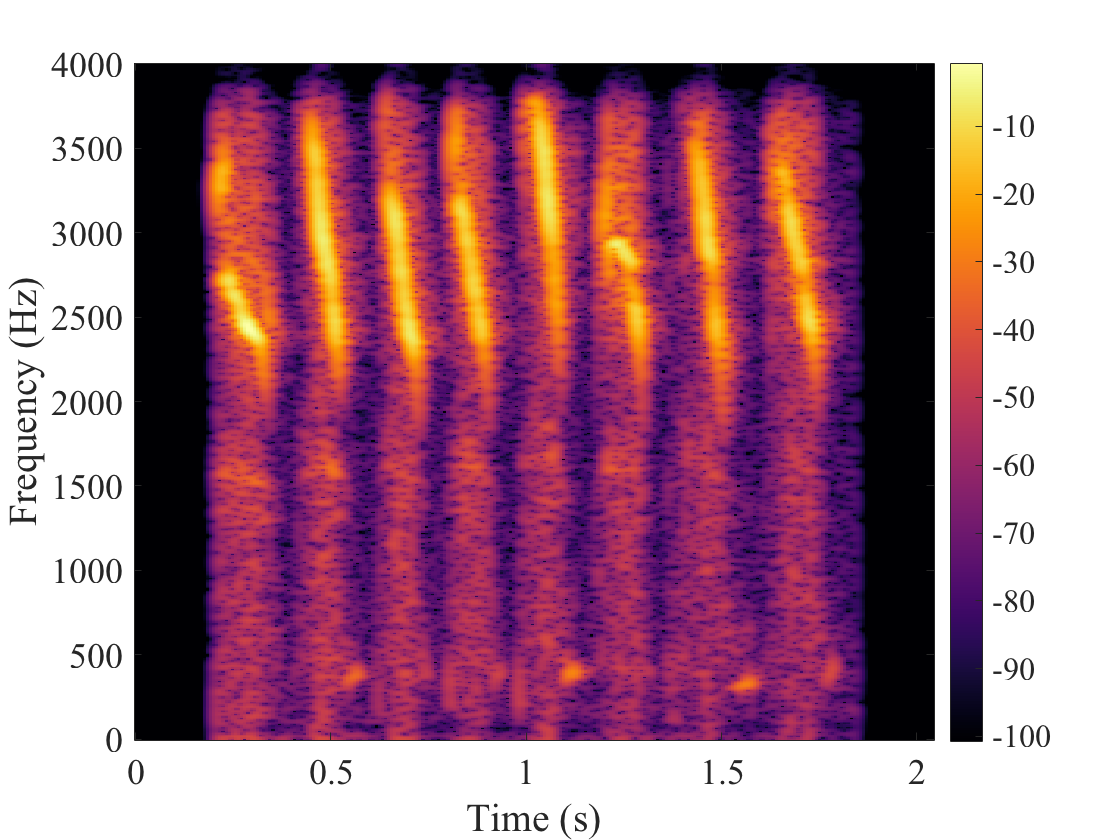
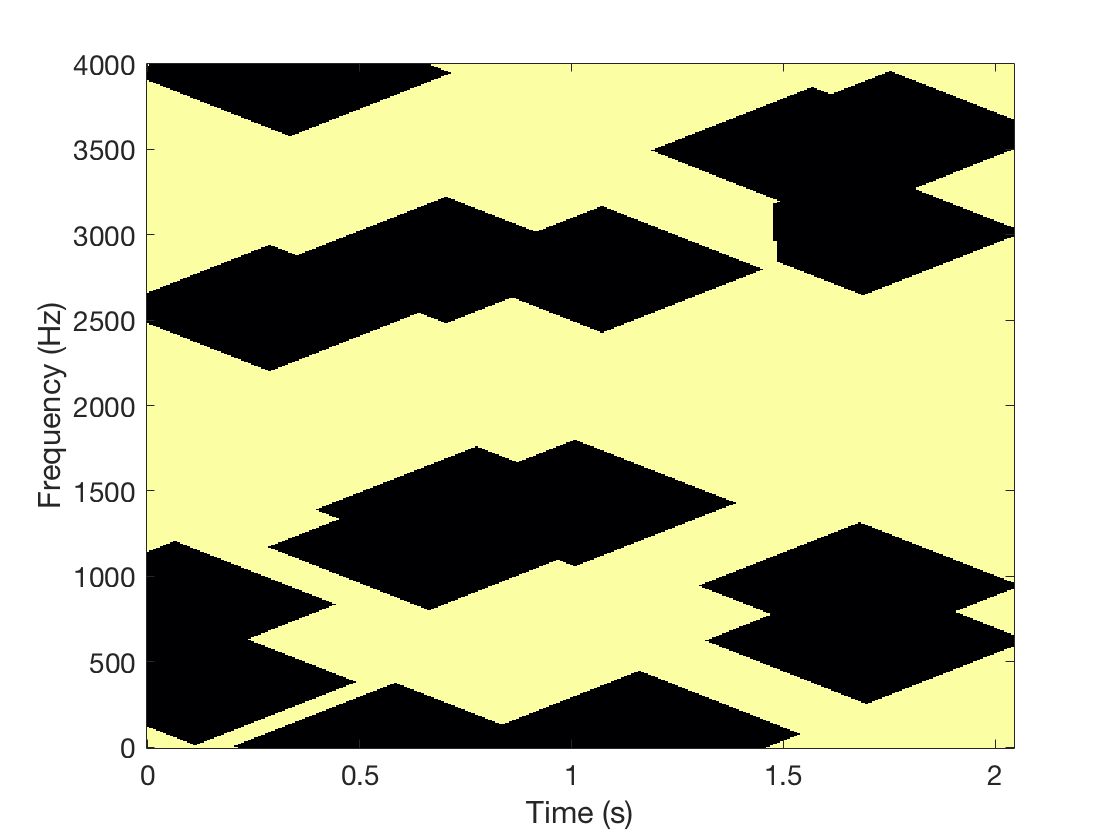
| Original sound | Signals with 40 % missing phases | RPI | GLI |
|---|---|---|---|
|
|
|
|
|